【游戏开发】排序算法之堆排序

2021-05-07

3482

父子节点的对应索引关系推导

假定我们拿到这样一个数组, 并且把它表示成以下的树结构

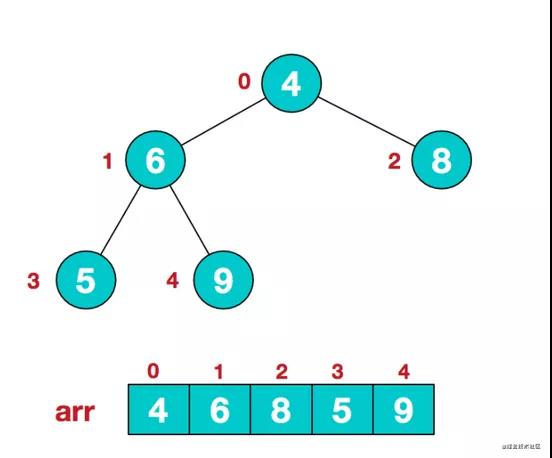
设:

P 是父节点对应数组的索引

C 是左子节点对应数组的索引

i 是子节点所在二叉树的层次

j 是子节点所在层次的偏移量

拿上图举例, P == 1(父节点 6), C == 3(子节点 5), i == 1, j == 1

可以推导:

C = 2 ^ i j P = 2 ^ (i - 1) (j - 1) / 2 P = ((2 ^ i j) - 1) / 2 = (C - 1) / 2

private int getParentIndex(int child) {
return (child - 1) / 2;
}
private int getLeftChildIndex(int parent) {
return 2 * parent 1;
}

如何构建一个最大堆

假设二叉树最后一层最后一个chaild是C

小于

大于等于

int last = arr.length - 1;

// 初始化最大堆, 找到C的parent, C的基础上减一递归找平衡
for (int i = getParentIndex(last); i >= 0; --i) {
adjustHeap(i, last);
}

private void adjustHeap(int i, int len) {
int left,
right,
j;
// 获取父节点i的左子
left = getLeftChildIndex(i);
// 如果i有子节点
while (left <= len) {
// i的右子
right = left 1;
j = left;
// 找出左右子最大的值
if (j < len && arr[left] < arr[right]) {
j ;
}
// 父节点小于子节点最大值
if (arr[i] < arr[j]) {
// 父子替换
swap(array, i, j);
// 替换后的父节点向下寻找看有没有比它大的子节点
i = j;
left = getLeftChildIndex(i);
} else {
break; // 停止筛选
}
}
}

算法思路

借助 数据结构-堆 的思想, 假定数组长度 n, 定义 i = n

最大堆

public static void sort(int[] arr) {
if (arr == null || arr.length <= 1) {
return;
}

int length = arr.length;
for (int i = getParentIndex(length - 1); i >= 0; i--) {
ajustHeap(arr, i, length - 1);
}

int i = length - 1;
while (i > 0) {
swap(arr, 0, i);
i--;
ajustHeap(arr, 0, i);
}
}

时间复杂度

O(nlogn)

初始化建堆过程时间：O(n) 更改堆元素后重建堆时间：O(nlogn) f(n) = n nlogn = n(logn 1) = O(nlogn)

推算过程：

首先要理解怎么计算这个堆化过程所消耗的时间，可以直接画图去理解；

假设高度为k，则从倒数第二层右边的节点开始，这一层的节点都要执行子节点比较然后交换（如果顺序是对的就不用交换）；倒数第三层呢，则会选择其子节点进行比较和交换，如果没交换就可以不用再执行下去了。如果交换了，那么又要选择一支子树进行比较和交换；

那么总的时间计算为：s = 2^( i - 1 ) * ( k - i )；其中 i 表示第几层，2^( i - 1) 表示该层上有多少个元素，( k - i) 表示子树上要比较的次数，如果在最差的条件下，就是比较次数后还要交换；因为这个是常数，所以提出来后可以忽略；

S = 2^(k-2) * 1 2^(k-3) 2….. 2 (k-2) 2^(0)*(k-1) ===> 因为叶子层不用交换，所以i从 k-1 开始到 1；

这个等式求解，我想高中已经会了：等式左右乘上2，然后和原来的等式相减，就变成了：

S = 2^(k - 1) 2^(k - 2) 2^(k - 3) ….. 2 - (k-1)

除最后一项外，就是一个等比数列了，直接用求和公式：S = { a1[ 1- (q^n) ] } / (1-q)；

S = 2^k -k -1；又因为k为完全二叉树的深度，所以 (2^k) <= n < (2^k -1 )，总之可以认为：k = logn （实际计算得到应该是 log(n 1) < k <= logn ）;

综上所述得到：S = n - longn -1，所以时间复杂度为：O(n)

更改堆元素后重建堆时间：O(nlogn)

推算过程：

1、循环 n -1 次，每次都是从根节点往下循环查找，所以每一次时间是 logn，总时间：logn(n-1) = nlogn - logn ；

完整代码：

class HeapSort {

public static void sort(int[] arr) {
if (arr == null || arr.length <= 1) {
return;
}

int length = arr.length;
for (int i = getParentIndex(length - 1); i >= 0; i--) {
ajustHeap(arr, i, length - 1);
}

int i = length - 1;
while (i > 0) {
swap(arr, 0, i);
i--;
ajustHeap(arr, 0, i);
}
}

private static void swap(int[] arr, int i, int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}

private static void ajustHeap(int[] arr, int start, int end) {
int left = getLeftChildIndex(start);
while (left <= end) {
int right = left 1;
int target = left;

if (right <= end && arr[left] < arr[right]) {
target = right;
}

if (arr[start] < arr[target]) {
swap(arr, start, target);
start = target;
left = getLeftChildIndex(start);
} else {
break;
}
}
}

private static int getParentIndex(int child) {
return (child - 1) / 2;
}

private static int getLeftChildIndex(int parent) {
return 2 * parent 1;
}

public static void main(String[] args) {
int[] array = {
111,
52,
77,
98,
36,
12,
13,
48,
79,
10,
6,
500
};
sort(array);
System.out.println(arrayToString(array));
}

private static String arrayToString(int[] array) {
StringBuilder builder = new StringBuilder();
for (int t: array) {
builder.append(t " ");
}
return builder.toString();
}
}

转载声明：本文来源于网络，不作任何商业用途。